Elliptic Curve Cryptography

Elliptic Curve

Assume a field $\Bbb{K}$, and the field's characteristic, $char(\Bbb{K}) \neq 2,3$, then an Elliptic Curve over the field can be described as the equation:

$E(x, y): y^2 = x^3 + ax + b$

There is a singular point $P(xp, yp)$, if

$$ \begin{align*} \frac{dE(x_p, y_p)}{dx} &= 3x_p^2 + a = 0 & \implies x_p & = (\frac{-a}{3})^{1/2} \newline \frac{dE(x_p, y_p)}{dy} &= 2y_p = 0 & \implies y_p & = 0 \newline \end{align*} $$

And substitute in $E(x,y)$

$$ \begin{align*} 0 &= (\frac{-a}{3})^{3/2} + a(\frac{-a}{3})^{1/2} + b \newline (-b)^2 &= ((\frac{-a}{3})^{3/2} + a(\frac{-a}{3})^{1/2})^2 \newline b^2 &= (\frac{-a}{3})^{3} + a^2(\frac{-a}{3}) + 2(\frac{-a}{3})^{3/2}a(\frac{-a}{3})^{1/2} \newline b^2 &= \frac{-a^3}{27} - \frac{a^3}{3} + \frac{2a^3}{9} = \frac{-4a^3}{27} \newline 27b^2 &= -4a^3 \newline 0 &= 4a^3 + 27b^2 \end{align*} $$

Such that if $4a^3+27b^2 \neq 0$ then the curve $E(x,y)$ is no-singular.

At last, here is the definition of elliptic curve:

$$ \{(x,y) \in \Bbb{K} \mid y^2 = x^3 + ax + b, 4a^3+27b^2 \neq 0\} \cup \{ \mathcal{O} \} \text{ if } char(\Bbb{K}) \neq 2,3 $$

with $\mathcal{O}$ the point at $\infty$. A group over elliptic curves can be defined as below:

the elements of the group are the points of an elliptic curve
the identity element is the point $\mathcal{O}$
the inverse of a point P is the one symmetric about the x-axis
addition: given 3 aligned, non-zero points P, Q and R, their sum P+Q+R=0

Addition

Given 3 aligned, non-zero points P, Q and R, their sum P+Q+R=0

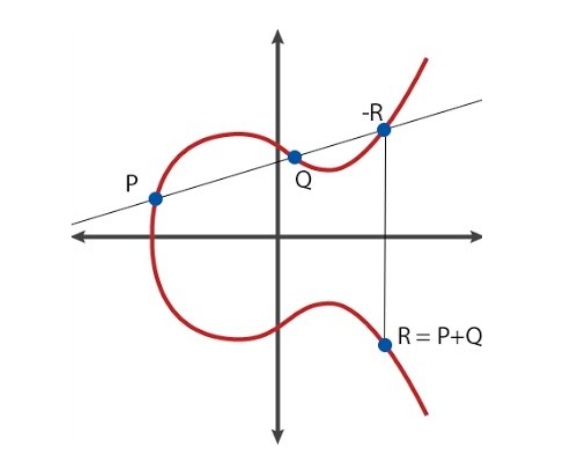
Elliptic curve (E): $y^2 = x^3 + ax + b$
Line (L): $y=mx+n$

The intersection points of (E) and (L) are the solutions to the equation below:

$$ \begin{align*} (mx+n)^2 &= x^3 + ax + b \newline m^2x^2 + 2mnx + n^2 &= x^3 + ax + b \newline 0 &= x^3 - m^2x^2 + (a-2mn)x + (b-n^2) \end{align*} $$

According to Vieta’s Formulas

$$ x_P + x_Q + x_R = -(-m^2) / 1 = m^2 $$

Assume 2 intersection points P, Q are already known, then the third intersection point -R, $P(xR, -yR)$,

$$ \begin{align*} x_R &= m^2 - x_P - x_Q \newline -y_R - y_P &= m(x_R - x_P) \newline \end{align*} $$

So the point R, $P(xR, yR)$:

$$ \begin{align*} x_R &= m^2 - x_P - x_Q \newline y_R &= -m(x_R - x_P) - y_P \end{align*} $$

If $xP \neq xQ$,

$$m=\frac{y_P - y_Q}{x_P - x_Q}$$

If $xP = xQ$

$$ \begin{align*} \frac{dy^2}{dx} &= \frac{d}{dx}(x^3+ax+b) \newline 2y\frac{dy}{dx} &= 3x^2 + a \newline \frac{dy}{dx} &= \frac{3x^2 + a}{2y} \newline & \implies \newline m & = \frac{3x_P^2+a}{2y_p} \end{align*} $$

Multiplication

$nP = P + P + ... + P$

Elliptic Curves over finite fields

In cryptography the finite field is usually a set of integers modulo $p$, where $p$ is a prime number. It is denoted as $GF(p)$ or $\Bbb{F}p$, and $char(\Bbb{F}p) = p$. Then an elliptic curve can be defined as:

$$ \{ (x,y) \in \Bbb{F}_p^2 \mid y^2 \equiv x^3 + ax + b \mod p, 4a^3 + 27b^2 \not\equiv 0 \mod 0 \} \cup \mathcal{O} $$

where $\mathcal{O}$ is still the point at $\infty$, $a$ and $b$ are two integers in $\Bbb{F}p$, and $char(\Bbb{F}p)=p \neq 2,3$

=== end ===

What is an elliptic curve cofactor?

https://crypto.stackexchange.com/questions/56344/what-is-an-elliptic-curve-cofactor

In cryptography, an elliptic curve is a group which has a given size n. We normally work in a subgroup of prime order r, where r divides n. The "cofactor" is $h=n/r$.

For every point $P$ on the curve, the point $hP$ is either the "point at infinity", or it has order $r$; i.e., when taking a point, multiplying it by the cofactor necessarily yields a point in the subgroup of prime order $r$.

SafeCurves: choosing safe curves for elliptic-curve cryptography https://safecurves.cr.yp.to/

Standard curve database

https://github.com/J08nY/std-curves
https://neuromancer.sk/std/

- P-384: https://neuromancer.sk/std/nist/P-384

What is an elliptic curve?

https://www.bilibili.com/video/BV1gN411o7un/?spmidfrom=333.337.search-card.all.click&vd_source=8d17b3ae547585ed3fea79027e6d20eb

Given a polynomial equation $f(x1, x2, ..., x_r) = 0$ with integer coefficients (i.e., a diophantine equation), we can ask three questions:

Can we determine if there are rational or integral solutions?
In the affirmative case, can we find such a solution?
Can we describe all such solutions?
(Hilbert's Tenth Problem over $Z$) Is there a Turing machine to decide if $f=0$ has solutions in $Z$ (Davis, Matiyasevich Putnam, Robinson: No) .

Examples of diophantine equation:

$9(x^2 + 7y^2)^2 - 7(u^2 + 7v^2)^2 = 2$

Elliptic Curve Point Addition

https://www.rareskills.io/post/elliptic-curve-addition

Cryptography uses elliptic curves over finite fields, but elliptic curves are easier to conceptualize in a real cartesian plane.

the identity element (which is the only element that can be the inverse of itself)

Elliptic curve point multiplication

https://en.wikipedia.org/wiki/Ellipticcurvepoint_multiplication

Constant time Montgomery ladder

The security of a cryptographic implementation is likely to face the threat of the so called timing attacks which exploits the data-dependent timing characteristics of the implementation.

Identity element https://en.wikipedia.org/wiki/Identity_element